CONTROLE COMMUN de MATHEMATIQUES
5ème : juin 2005

 CORRIGE

ALGEBRE

Exercice 1

1°) Calculer en respectant les priorités 

A = 138 – 8 ´ 9 = 138 -72 =  66

2°) Calculer de deux façons différentes :

B = 8 ´  ( 125 – 50 ) = 8 × 75 = 600

B = 8 ´  ( 125 – 50 ) = 8 × 125 - 8 × 50 = 1000 = 400 = 600

3°) Calculer astucieusement :

D = 87 × 99 = 87 × ( 100 - 1 ) = 87 × 100 - 87 × 1 = 8700 - 87 = 8613

4°) Calculer:

J = (+18) – (-7) + (+9) – (-3) + (-8) = 18 + 7 + 9 + 3 - 8 = 37 - 8 = 29

Exercice 2

1°) Simplifier les fractions: 

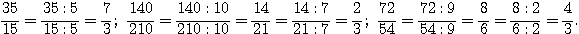
2°) Calculer et simplifier si possible :

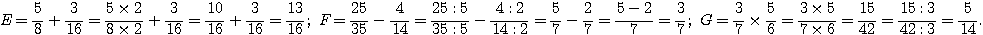
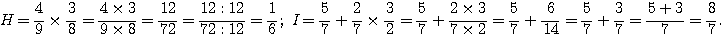
Exercice 3

Stéphane a un revenu mensuel de 1400 €.

Son loyer représente 3/7 de ses revenus et la nourriture 1/4 de ses revenus.

a) Montant de son loyer : 3/7 de 1400 = 3×1400 / 7 = 4200 : 7 = 600 €

b) Montant de sa nourriture: 1/4 de 1400 = 1400 : 4 = 350 €.

c) Il lui reste: 1400 - ( 600 + 350 ) = 1400 - 950 = 450 €

Exercice 4

Complétez le tableau :

Exercice 5

Le coefficient de proportionnalité est 27 : 5 = 5,4  

GEOMETRIE

Exercice 1

En utilisant la figure ci-dessous et en justifiant:

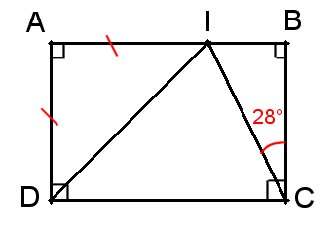
a) IBC est rectangle en B donc BÎC = 90 - 28 = 62°

b) Les angles ICD et BÎC étant complémentaires, ICD = 90 - 28 = 62°

c)  AID est un triangle rectangle isocèle, donc AÎD = 45°.

d) AÎB est plat, donc DÎC = 180 - ( 62 + 45 ) = 180 - 107 = 73°.

Exercice 2

Calculer l’aire des figures ci-dessous (on considère que 1 carreau = 1cm)

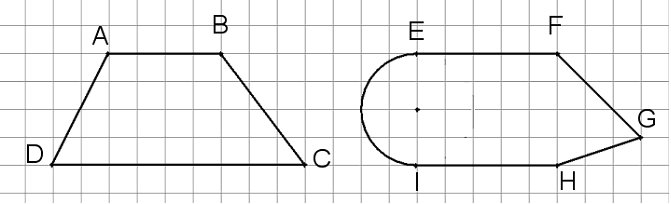
Aire de ABCD: aire d'un trapèze = (B+b) × h / 2 = ( 9 + 4 ) × 4 / 2 = 13 × 2 = 26 cm².

Aire du demi disque de diamètre [EI] :  П× R² / 2 = 3,14 × 2² / 2 = 6,28 cm²
Aire du rectangle EFHI: L × l = 5 × 4 = 20 cm²
Aire du triangle FGH: b × h / 2 = 4 × 3 / 2 = 6 cm²
Aire de la seconde figure: 6,28 + 20 + 6 = 32,28 cm²

Exercice 3

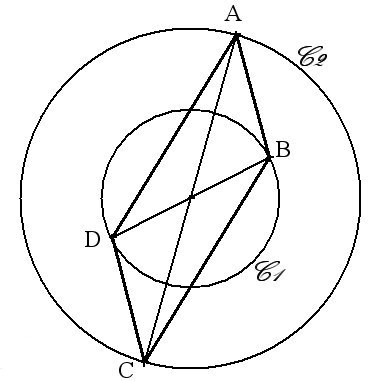
Quelle est la nature du quadrilatère ABCD ci-dessous?

[AC] est un diamètre du cercle C2 de centre O; [BD] est un diamètre du cercle C1 de centre O.

Les diamètres [AC] et [BD] se coupent en leur milieu O, donc ABCD est un parallélogramme.

Exercice 4

Construire en rouge le symétrique de la figure par rapport au point I et construire en bleu le symétrique de la figure par rapport à la droite d.