
ARITHMETIQUE
1°) Nombres rationnels
Les nombres rationnels sont les nombres qui peuvent s'écrire sous forme d'une fraction a/b.
On trouve parmi les rationnels:



Remarque, la forme décimale d'un rationnel est toujours
répétitive, on dit qu'on observe une période
exemple: 2/7 = 0,28571428571428571428571428571429...
285714 est la période
Par contre, un nombre irrationnel n'est pas le résultat d'une fraction, la partie décimale n'est pas périodique.
Par exemple: ![]() = 3,141 592 653 589 793 238 462 ... 3,141 592 653 589 793 238 462 ... est
irrationnel.
= 3,141 592 653 589 793 238 462 ... 3,141 592 653 589 793 238 462 ... est
irrationnel.
2°) Diviseurs communs, PCGD.
Considérons les nombres entiers 120 et 48.
On recherche
tous les diviseurs de 120 et tous les diviseurs de 48:
|
Diviseurs de 120: |
Diviseurs de 48: |
|
1 × 120 |
1 × 48 |
On remarque que les diviseurs communs à 120 et 48
sont: 1; 2; 3; 4; 6; 8; 24.
Parmi ces diviseurs communs, le plus grand est
24.
On dit que 24 est le PGCD (plus grand commun diviseur) de 120
et 48.
3°) Recherche du PGCD
Pour rechercher le PGCD de deux nombres, il existe deux méthodes rapides, en plus de la recherche systématique de tous les diviseurs communs.
a) Méthode par soustractions
"Si on nombre divise à la fois a et b, il divise aussi
leur différence".
En partant de cette propriété, on applique la méthode
de soustractions successives.

Le PGCD doit diviser 120 et 48 et donc aussi 120-48, c'est à
dire 72 et 48.
On recommence en calculant 72 - 48 , puis 48 - 24 et ainsi
de suite en prenant toujours les deux derniers résultats.
Le dernier résultat
non nul est donc obligatoirement le PGCD (ici 24).
Deuxième exemple, recherche du PGCD de 84 et 60:

Le PGCD de 84 et 60 est donc 12.
b) Méthode par divisions (algorithme d'Euclide)
Le même type de raisonnement s'applique aussi avec des divisions
successive...
Exemple, recherche du PGCD de 120 et 48 par divisions:
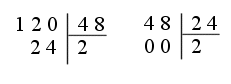
On divise 120 par 48; puis 48 avec le reste 24...
Le dernier
reste non nul, 12, donne le PGCD.
Deuxième exemple: recherche du PGCD de 165 et 105

Le PGCD de 165 et 105 est donc 15.
4°) Nombres premiers entre eux, fraction irréductible
Lorsque le PGCD de deux nombres est 1 on dit qu'ils sont premiers
entre eux.
C'est-à-dire qu'ils n'ont pas de diviseurs communs.
En particulier, si on divise deux nombres par leur PGCD, on
obtient des nombres premiers entre eux.
Exemple: le PGCD de 120 et 48 est
24 120 : 24 = 5 et 48 : 24 = 2 .
5 et 2 n'ont pas
de diviseurs communs, ils sont premiers entre eux.
Ceci peut être très utile pour simplifier des fractions en divisant le numérateur et le dénominateur par leur PGCD.

La fraction 2/5 n'est plus simplifiable, on dit qu'elle est irréductible.
4°) Exercices
a) Calculer le PGCD de 817 et 513
b) Calculer le PGCD de 495 et 315
c) Les nombres 168 et 715 sont-ils premiers entre eux (répondre par oui ou non )?
d) Les nombres 273 et 385 sont-ils premiers entre eux?